Endgame Perils of Restaking
Fear not that restaking protocols might fail, but that they could succeed.
TL;DR
Restaking protocols may provide significant financial benefits to validators, but their success has the potential to compromise Ethereum’s ability to self-regulate staking participation and to temper centralizing forces. We believe that the logical endgame is an ingrained cap on the size of the active validator set.
The economic case for Lido choosing to self-limit their validator set is examined, and we find that restaking protocols will likely make the option unfeasible.
Ethereum’s long-term challenge is not to get more people to stake, it’s to get less people to stake.
A common belief among the less-initiated is that the endgame of Ethereum will see staking participation join the likes of Solana and Cardano; both chains having approximately 70% of their token supplies staked and inactive. However, there is deep consensus in the Ethereum research and development communities that this is not a good outcome.
In a sense, Bitcoin Maximalists are correct about Ethereum’s monetary policy: it is not set in stone and may change in the future. They are however wrong about the direction; rather than Ethereum hyper-inflating, there is a strong possibility that demand to stake will climb well above target and rewards will drop—token holders may be rugged by the Ethereum Foundation into their asset having even stronger monetary properties1.
Readers who are stuck in a fiat (or bitcoin) mindset may view additional stakers as a net positive for Ethereum, but one should recall that proof-of-stake inverts monetary policy dynamics. Higher issuance (and thus staking yield) doesn’t make holders less likely to HODL their tokens; it encourages holders to stake their assets and realize that higher APR.
For example, people claim that EIP-1559 is a NGU (number go up) ultra sound money scheme, but in really it actually lowers staking APR and encourages network activity rather than staking/holding.
Restaking protocols, such as EigenLayer, which offer yield external to the Ethereum protocol, distort market incentives and undermine Ethereum’s monetary policy controls. These protocols paint a concerning picture of a possible hyper-financialized endgame for the cryptoasset.
The Monopolistic Dynamic
Ethereum’s monetary policy includes an embedded negative feedback loop to discourage staking from overwhelming other use cases: as more people lock their tokens in the deposit contract, the yield decreases. This disincentivizes additional staking activity and lowers the opportunity cost of choosing to use the chain.
One method that I’ve found useful for analyzing this feedback loop is to imagine stakers of various chains as a single or small group of monopolistic actors, and then calculate the optimal amount of real yield they could extract from non-stakers, and the share of supply that they would lock up to achieve it2.
I’ve discussed this profile in the past, but to briefly remind the reader of how the extracted real yield curves work, we should start by realizing that staking rewards come purely from the dilution of other holders and validators. If a single actor were to own and stake every ether in circulation, they would simply be self-diluting and would therefore earn zero real yield. Likewise, if there were no stakers securing the network, then there would be no one earning yield. These two boundary conditions at 0% and 100% of supply staked imply a maximum point of yield extraction that we plot in the figure above.
Any deviation from this peak represents sub-maximal taxation of non-stakers. If we expect a monopolist staking cartel to occupy this share of the supply, then opening competition to others will logically push the staking equilibrium further out the curve. As such, we see the peak in the figure above, at approximately 33%, as a minimum of where the free market could push staking participation in the long-term.
In stark contrast to Ethereum’s issuance schedule, Solana’s issuance is pre-set and independent of the number of validators. Therefore, to maximize extraction, a monopolist staker would ideally hold as little of the supply as possible (in order to minimize self-dilution). However, in practice everyone is able to delegate their stake with little barrier to entry, and as issuance happens regardless and the ecosystem is still under development we observe a very high participation rate.
The Role of Costs and Risks
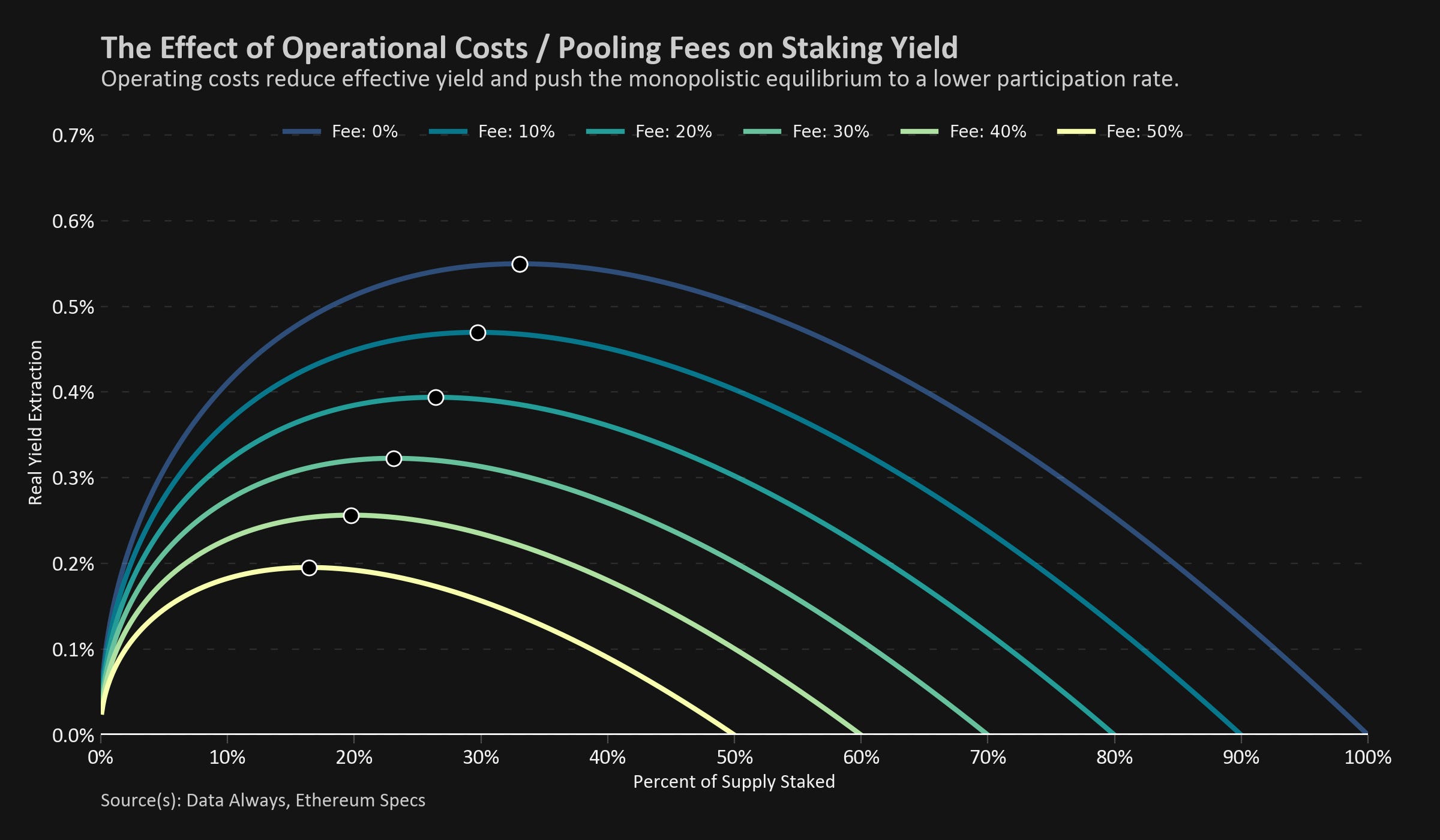
This analysis primarily discusses factors that increase staking yield, but it’s essential to note that operational costs and risk adjustments are equally important factors in the conversation. The risk profile of staking will change signfinicantly after the Shaghai update, at which point a more nuanced discussion might be appropriate3.
For this analysis, we will incorporate operational costs and risk adjustments by allowing the reader to choose a rate to discount their yield. This provides some flexibility; for example, a 25% fee rate could represent a staking fee on a centralized exchange, a liquid staking token (LST) with a 15% fee rate and an additional 10% discount for contract risk, or a discount for a home staker who might encounter any type of issue.
One detail to recall is that fees are charged in nominal terms, but the yield that stakers should be interested in is measured in real terms. When we adjust for fees, real yield no longer converges to zero, but instead it goes negative at high fee rates or high staking participation. The disconnect between nominal fees and real earnings shifts the monopolistic equilibrium to a lower participation rate.
In the figure below, we generate profiles for various fee rates4.
Before validator withdrawals are enabled one could argue that a discount rate near 50% is appropriate, but we do not mean to suggest that the ecosystem is currently near a meaningful equilibrium.
Restaking and the Role of External Yield
The term restaking has been used to describe various activities in the staking ecosystem. When one is discussing LSTs, like Lido’s stETH or Rocket Pool’s rETH, restaking usually refers to staking rewards being fed back into the ecosystem in order to create more validators and compound the yield earned by the protocol. Alternatively, restaking was often a term to describe the looped stETH trade that spiraled out of control in early 2022. Firms would deposit ether with Lido to get stETH, and then borrow against those stETH tokens to gain leverage and re-stake to earn additional yield. This analysis is not a discussion of either of those methods of restaking.
Today, restaking most often refers to protocols like EigenLayer, which are a series of smart contracts that allow Ethereum stakers to re-pledge their collateral to secure secondary applications or protocols. By opting-in to custom additional slashing conditions defined by smart contracts, stakers will soon be able increase their APR with yield external to Ethereum’s monetary policy. If this concept is new to you, I would recommend the following:
The EigenLayer Whitepaper.
Consensys’s description of the protocol.
The key difference between restaking through a protocol like EigenLayer or using a looped LST trade is the idea of internal vs external yield. Although both methods increase yield and risk, looped staking is tempered by the negative feedback loop embedded in Ethereum’s monetary policy. In contrast, the Ethereum protocol has no way to discourage the use of external yield protocols.
The result is that looped staking moves the equilibrium to a lower percent of supply staked, while external restaking moves the equilibrium to a higher percent of supply staked5.
The results are striking when we model the evolving equilibrium for different external restaking yields. Since external yield is not self-dilutive, even small amounts of added yield may have a drastic effect on the staking ecosystem. If protocols like EigenLayer are able to generate a sufficient supply of external yield at just 1%, the optimal staking dynamic could be pushed to untenable levels.
The Ethereum research community has often seen the adoption of minimum viable issuance as the key to discouraging high staking participation rates. The idea is that if too many people want to stake, lowering the yield will make staking less attractive, while also improving the monetary properties of the cryptoasset.
A minimum viable issuance policy might still have the desired effect due to the competitive nature of the network, but in a monopolistic optimization problem restaking reverses the result. In this dynamic, lowering protocol issuance decreases the effect of self-dilution and encourages the monopolist to stake more tokens and take advantage of the external yield.
To reclaim the monopolistic equilibrium and lower the optimal staking level for large actors, the correct game theoretical move shifts to increase staking APR—making the taxation of other holders more valuable than the restaking rewards.
It’s possible that low issuance and high participation is an acceptable outcome for the network, in turn outsourcing the subsidization of security to other protocols, but it will be important to monitor for changes in the centralization of staking. If, for example, Lido integrations with EigenLayer are the most desired by the market it’s possible that minimum viable issuance could be a nonviable solution.
Concluding Thoughts
Restaking protocols distort the intrinsic staking feedback loop. It’s possible that, in the long-term, Ethereum will no longer be able to fight both high staking participation and centralizing forces by modifying the APR of rewards.
The nuclear solution to the problem has been discussed for years, and Data Always believes that a cap on the active validator set will eventually need to be implemented. To follow the discussion going forward, one should focus their attention on Ethereum’s Robust Incentives Group, and the work done by Anders and Barnabé on auctioning off validator slots.
Addendum: Lido Self-Limiting
The analysis can be extended to model the economic costs associated with Lido, the largest LST provider, choosing to self-limit its share of the network. The social argument has been debated meticulously, but when a proposal was raised in the community it was overwhelmingly rejected (99.8% against).
To analyze the economic argument we need to consider the three classes of stakeholders and each of their incentives:
The LidoDAO who receives 10% of all staking rewards for their treasury.
Although individual members of the DAO should have aligned incentives with holders of stETH, the DAO itself has a different reward optimization than the holders. Because the DAO does not have exposure to the underlying ether tokens used in validators, it should seek to maximize nominal, not real earnings. The DAO should aim to absorb all ether it can because it is not required to keep its funds in ether, and self-dilution can thus be minimal.
Individual holders of stETH.
Individual holders of stETH should generally not change their actions in fear of self-dilution. Acting as individual chunks of the stETH supply, increasing one’s validating assets acts to dilute the entire network (including stETH holders). All individual holders should be well below any optimal point, meaning that their increase in share is net-positive to their rewards even if it drives the total pool of stETH past its optimal point.
The cumulative pool of stETH holders.
We would argue that the primary responsibility of the LidoDAO should be to the total pool of stETH holders. If adding new validators has the net-effect of diluting the total stETH set more than the marginal rewards (ie: adding more validators decreases the total real rewards extracted by stETH holders) then the DAO should refuse to issue more stETH and should self-limit.
We can modify the methodology presented in this analysis to model the effect of non-Lido validators on the staking yield of Lido validators, but we will only consider self-dilution from additional Lido validators in the optimization, rather than the real yield extraction of the total network.
In the figure below, we apply Lido’s 10% fee on rewards while creating non self-dilutive yield extraction profiles based on fractions of the total ether supply staked by non-Lido validators.
As more non-Lido staking occurs, the shape of the yield curve pushes Lido’s optimal staking amount lower. This is another feedback loop: more non-Lido staking means that Lido as a whole should want to absorb less ether.
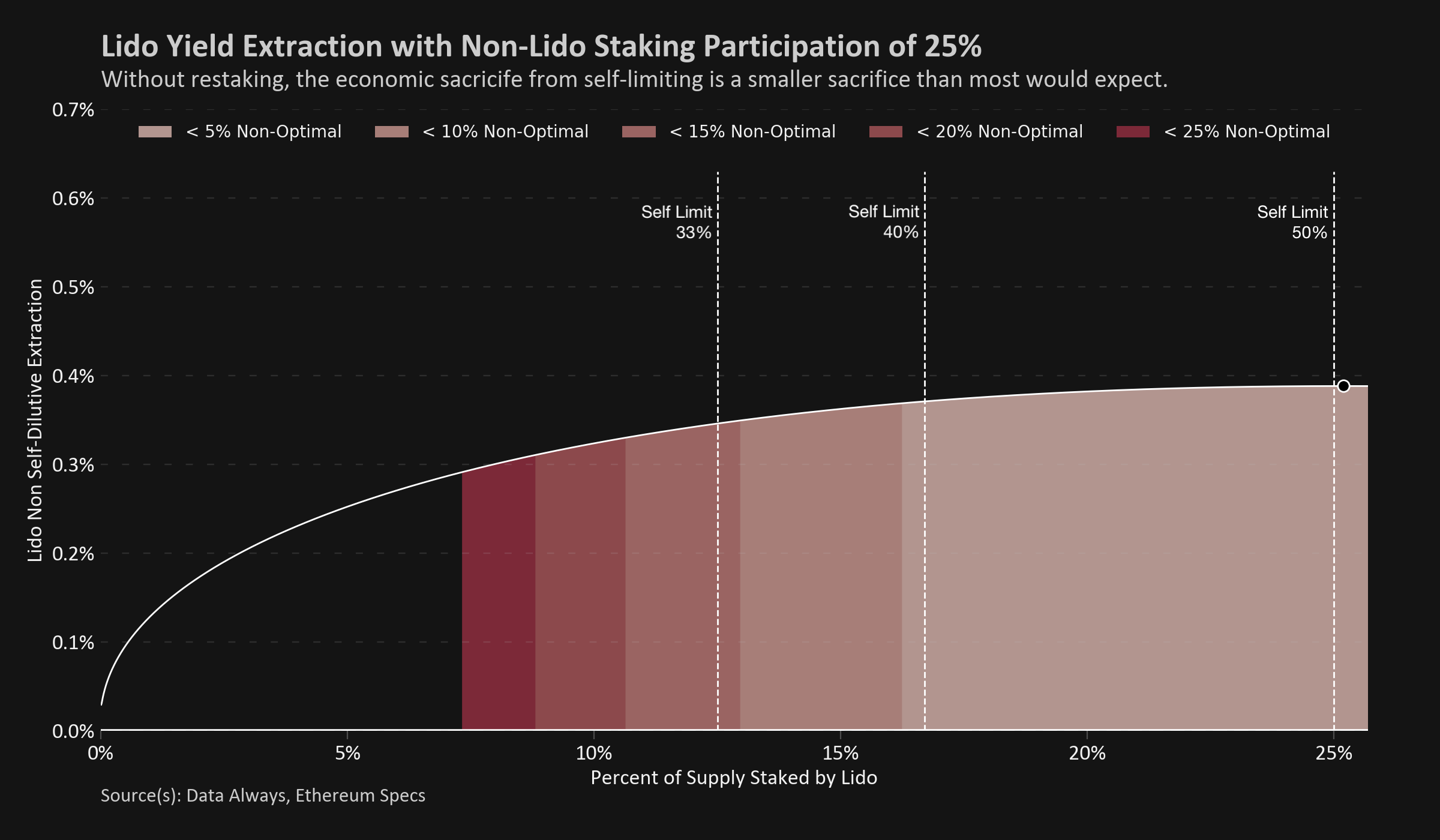
Diving another layer deeper, we can analyze a specific Lido profile for a given non-Lido staking participation (in this case 25%). One thing worth noting is that near the optimal point the curve is relatively flat, which suggests that the cost of staying close but away from the peak is relatively low.
Assuming that 25% of the total ether supply is staked by non-Lido validators, to optimize the yield extraction by the stETH holder set, Lido should aim to capture 25.2% of the token supply. This would put them at 50.1% of validators, far from ideal outcome for the network as a whole. With a very small sacrifice, Lido could chose to self-limit below 50% of the network and sacrifice less than 1% of real earnings.
A self-limit that most non-Lido community members would prefer is the 33% threshold; this would keep them below 12.5% of the total ether supply, but would have the effect of decreasing their optimized earnings by 11%. Note that this wouldn’t mean stETH holders would earn less (in fact, each stETH token would earn more than it would at the optimal point), but the total Lido validator set would extract 11% less real profit from non-stETH holders.
Restaking protocols drastically distort the incentive structure. If protocols like EigenLayer can generate even just a 0.5% nominal yield, then anything more than majority self-limiting becomes nonviable. Choosing to self-limit below 33% of the staking share sacrifices over a quarter of the potential earnings for the set of stETH holders.
The community cannot reasonably expect LidoDAO to make such a large sacrifice in the free market. In this case, the community should focus on ensuring that the Lido validator set is sufficiently decentralized and that the DAO exerts as little control as possible over the operators.
This article now has a second addendum that was added to address feedback and weaknesses of the original version. It is it’s own document available at the link below.
Thank you to Jon Charbonneau and Walt Smith for their invaluable feedback on early drafts. This writing does not necessarily reflect their views on the subject.
Proposals around burning MEV are adjacent, but the results are similar. If MEV burn is implemented, it will decrease staking APR (and hence demand) and may delay the need to reduce staking rewards.
Ethereum staking issuance rates do not have knowledge of the total supply of ether, only of the size of the validator set. To simplify the analysis for the reader, we assume that the total supply of ether is fixed at 120.4 million tokens.
We would love to see someone else do this, happy to help if you reach out.
To generate a curve from this figure we need to start with finding the real yield of a validator.
RealYield = APR - Inflation
I like Ben Edgington’s approximations for simple math like this:
APR = 29.40 / sqrt(N) where N is the number of validators.
To convert this to network share we assume that the supply of ether is 120.4 million and recall that each validator has 32 ether in it. In the formula below S represents the effective network share of validators.
APR = 29.40 / sqrt(120.4 × 10^6 / 32 × S) = 0.01518 / sqrt(S)
Inflation is then the APR multiplied by the effective network share of validators.
Inflation = APR × S = 0.01518 × sqrt(S)
We can now calculate the real yield:
RealYield = 0.01518 / sqrt(S) - 0.01518 × sqrt(S)
If we want to incorporate a fee adjustment we multiply the APR by (1 - F), but leave the inflation untouched. As the Fee (F) goes to zero, we recover the initial real yield.
RealYield = (1 - F) × 0.01518 / sqrt(S) - 0.01518 × sqrt(S)
To create a profile of the extracted real yield (ERY) we then multiply the real yield by the effective network share of validators:
ERY = RealYield × S = (1 - F) × 0.01518 × sqrt(S) - 0.01518 × S^(3/2)
ERY = 0.01518 × ((1 - F) × sqrt(S) - S^(3/2))
We can then solve for the highest points on the curves by taking the derivative of the extracted real yield curve and finding its roots/zeros.
dERY/dS = 0 when S = (1 - F) / 3
This curve S = (1 - F) / 3 represents the validator network share to extract the highest amount of funds from non-validators assuming a discount or fee rate of F.
These profiles assume that there is far more demand for restaking than there is today, but in time who knows.